|
|
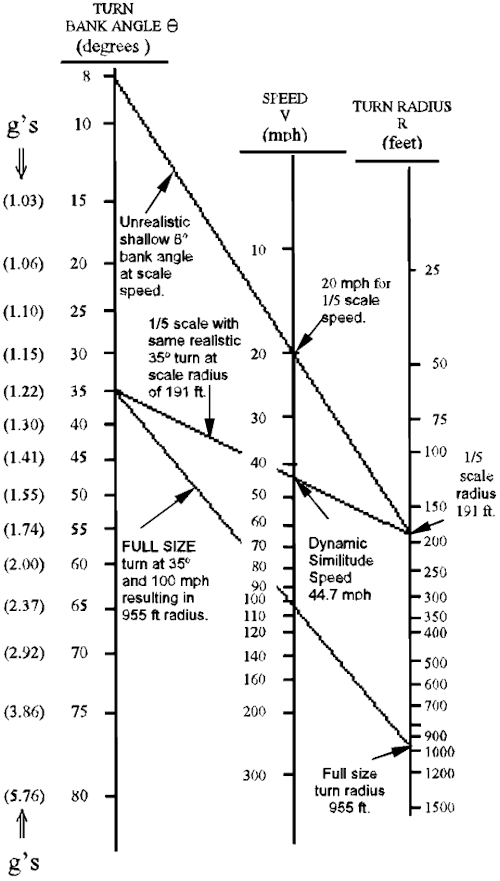
FIGURE 1.Coordinated
Turn Nomograph. By drawing a straight line between any
two items,
the third feature of the turn can be determined. |
|
With any two features the third can be determined for full-size as
well as any selected scale-size model or maneuver we might wish to
compare. If we use a 35 degree bank-angle example for a full-size
general aviation aircraft flying at 100 mph (or 146 ft/sec), we can
easily find it will turn in a radius of 955 ft. This is simply done by
drawing a line between the 35 degree bank angle on the left to 100 mph
in the middle and then extending the same straight line to the right
side of Figure 1 for turn radius. The same 35 degree bank angle can
then be used to also find the correct speed for a scale-size turn of
1/5 radius (955/5) or 191 feet to show a model speed of 44.7 mph
(DSS). If we try to fly at a scale speed of 100mph/5 or 20 mph for
this same scale-size radius of 191 ft, we can verify the earlier
described unrealistic 8 degree bank angle occurs from this nomograph.
Further benefits exist from Dynamic Similitude
Speeds when compared to slower scale speeds. We can determine that DSS
improves Reynolds' Number (RN), since RN is proportional to both speed
and wing-chord-scale size. Suffice it to say Reynolds' Number is
already significantly reduced or compromised from smaller scale wings
in modeling. It should not be dangerously handicapped further by lower
scale speeds compared to DSS. This perhaps acknowledges that we can
scale the size of our model, but not the distance between the air
molecules we fly through to sustain flight. Since our smaller models
fly in comparatively "thin or expanded air", excessively
slow speeds (such as scale speeds) can easily invite stalls. In
straight flight, better stability and improved realistic lower angle
of attack is also achieved with DSS to avoid stalls compared to those
required using slower scale speeds. Modelers may build light-weight
models to minimize stalling speeds from this environmental feature,
but this will do nothing to achieve other maneuver realism features if
attempted with scale speeds compared to DSS.